k短路径问题 问题描述 给出一个图，由n个点和m条边组成，给定起点s和终点t，求s到t的第k短路径，图中每个点包括起点和终点都可以多次经过。

输入 第一行输入两个整数n，m其中1<=n<=1000, 1<=m<=100000;点从1~n开始编号，之后的m行中每行输入三个整数a,b,w，代表a到b之间有一条单向变，长度为w，最后一行输入三个整数s，t

，k。

输出 输出s到t的第k短路径的长度。

问题分析 如何求第k短路径 我们先解决一个基础问题，如何求第k短路径，之前都是求最短路径，如果bfs算法中第一次搜索到终点时那么就是最短路径，那么同理，如果bfs算法中第k次搜索到终点时那么这个就是它的第k短路径，可以用一个计数变量实现这一算法

如何实现A算法 实现A算法的关键就是设计f(i)函数，其中g(i)函数是到起点的最短路径，h(i)是到终点的理论最短路径，那么h(i)就可以事先用dijkstra算法求出终点到图中各个点的最短路径，从而实现A*算法 dijkstra算法 这个算法相当于在传统的bfs算法的基础上加上优先队列，是一个可以搜索起点到每个节点的最短路的最短路径的算法，由于使用了优先队列，使得它可以处理边权不同的图问题

A*算法 这才是这个blog的重点，前面说到传统bfs算法是盲目的，但如果我们可以事先知道，走哪条路径是最优的，那么每次都取最优的方向开始搜索，这不就给算法赋予了方向感了吗。

    大家可能已经注意到了，每次去最优的方向，这不就是贪心算法的思路吗，但肯定也有人听过，贪心算法得出的答案不一定是最优的，如果是在没有任何障碍的方格图中，贪心算法是最优的，但如果是其他情况，那就不一定了，我们已知dijkstra算法得出的答案一定是最优的，那么是否可以将两种算法结合一下，那么既可以保证算法的正确性又提升了算法的执行效率，答案是肯定的，这也就得出了A*算法。

    A*算法=dijkstra算法+贪心算法。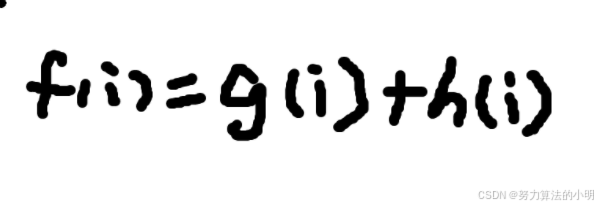

    贪心算法每次优先入队的是距离终点最近的节点，dijkstra算法每次入队的是距离起点最近的节点，那么A*算法就可以每次优先入队距离起点距离+距离终点距离最小的节点，假设起点为s终点为t，起点到达i节点后优先入队s->i+i->t最小的节点。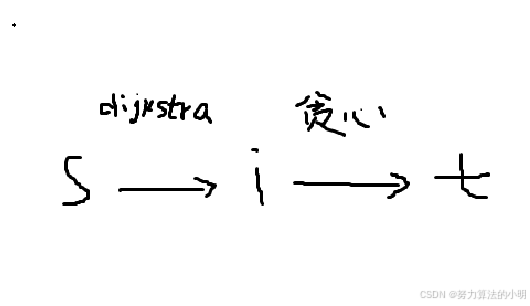

    现在我们来说明A*算法的正确性，如果到达终点时入队的时s->i+i->t最小的节点，由于i->t为0那么入队的就是s->t最小的节点，这个就是答案

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1010;
const int M = 1000010;
typedef pair<int, int> P;
 
struct Data{int v, h, g;}fr, nx;
struct Edge{int to, next, cost;} e[M * 2];
int d[N];
int vis[N];
int first[N];
int tu[M], tv[M], tw[M];
int cnt[N];
int n, m;
int s, t, k;
int tot = 0;
int res;
 
void addedge(int v, int u, int w){
    ++tot;
    e[tot].to = u;
    e[tot].cost = w;
    e[tot].next = first[v];
    first[v] = tot;
}
 
void dijkstra(int s){
    memset(d, 63, sizeof(d));
    memset(vis, 0, sizeof(vis));
    d[s] = 0;
    priority_queue<P, vector<P>, greater<P> > qu;
    qu.push(P(0, s));
    while(!qu.empty()){
        P p = qu.top();
        qu.pop();
        int u = p.second;
        if(d[u] < p.first) continue;
        for(int i = first[u]; i != -1; i = e[i].next){
            int v = e[i].to;
            if(d[v] > d[u] + e[i].cost){
                d[v] = d[u] + e[i].cost;
                qu.push(P(d[v], v));
            }
        }
    }
}
 
bool operator < (Data x, Data y){
    return x.g + x. h > y.g + y.h;
}
 
void getK(int s){
    priority_queue<Data> Q;
    fr.v = s;
    fr.g = 0;
    fr.h = d[s];
    Q.push(fr);
    while(!Q.empty()){
        fr = Q.top();
        Q.pop();
        //cout << "fr.v = " << fr.v << " " << fr.g << " " << fr.h << endl;
        if(++cnt[fr.v] > k) continue;
        if(cnt[t] == k){
            printf("%d\n", fr.g + fr.h);
            return;
        }
        for(int i = first[fr.v]; i != -1; i = e[i].next){
            int u = e[i].to, w = e[i].cost;
            nx.v = u;
            nx.g = fr.g + w;
            nx.h = d[u];
            //cout << "nx " << nx.v << " " << nx.g << " " << nx.h << endl;
            Q.push(nx);
        }
   }
   puts("-1");
   return;
}
 
int main(){
    while(scanf("%d%d", &n, &m) != EOF){
        memset(first, -1, sizeof(first));
        tot = 0;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &tv[i], &tu[i], &tw[i]);
            addedge(tu[i], tv[i], tw[i]);
        }
        scanf("%d%d%d", &s, &t, &k);
        if(s == t) k++;
        dijkstra(t);
        //for(int i = 1; i <= n; i++) cout << d[i] << " "; cout << endl;
        tot = 0;
        memset(first, -1, sizeof(first));
        for(int i = 0; i < m; i++)
            addedge(tv[i], tu[i], tw[i]);
        memset(cnt, 0, sizeof(cnt));
        getK(s);
    }
    return 0;
}
 
/*
3 3
1 2 1
2 3 2
1 3 4
1 3 2
 
3 4
1 2 1
2 3 2
1 3 4
3 1 4
1 3 3
 
2 3
1 2 5
1 2 6
2 1 4
1 2 2
 
 
2 4
1 2 1
1 2 2
1 2 3
2 1 5
1 2 3
 
2 4
1 2 1
1 2 2
1 2 3
2 1 5
1 2 4
 
2 4
1 2 1
1 2 2
1 2 3
2 1 5
1 2 5
*/