之前的半平面交一直建立在多边形的基础上，因此遇到更一般的线性规划就显得有点措手不及。。

先讲一下线性规划的思路吧：

首先是把方程转化为半平面，这对用n^2的人来说并不难。。他们只需要用到直线方程。。

然而对使用nlogn的人来说，需要的反而是直线上的2点，这种逆变换感觉并没有什么优雅的姿势去解决。。

窝是这么解的。。首先先找出半平面的方向，即倾斜角k。。然后再找特殊点，在特殊点的基础之上分别加上cost和sint即可。。

然后倾斜角t要怎么找。。这里用图解可能会方便点。。。以Ax+By+C<0为例：

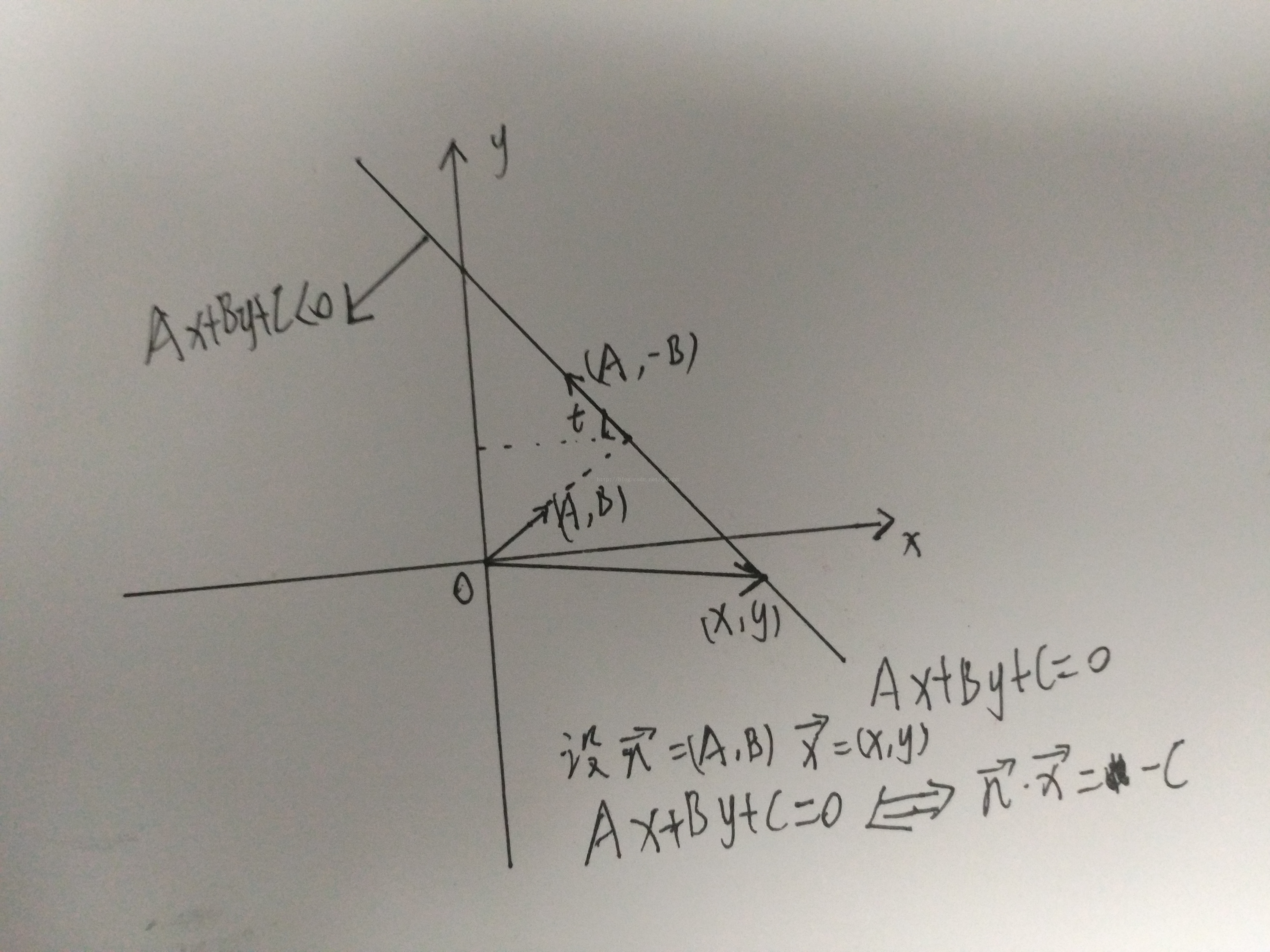
这里用到了直线方程的另外一种理解，点乘为定值的集合，这样可以通过向量n迅速找到和t的关系，将n旋转90度后倾斜角就已经是t了，所以t=atan2(-B,A)

特殊点窝取了y=0，考虑直线和y垂直的情况，需要特判一下才能取特殊点。。

转化为半平面后直接半平面交吧。。

设3个路程分别为a,b,c的话。。题目的要求应该是对每个人t，看是否满足

a/u[t]+b/w[t]+c/v[t]<=a/u[i]+b/w[i]+c/v[i] i=1~n

当且仅当i==t等号成立

然后发现是3个未知数。。怕不是要来个三维的。。

其实很容易发现该式是个齐次式，同除c可以得到

a/c/u[t]+b/c/w[t]+1/v[t]<=a/c/u[i]+b/c/w[i]+1/v[i]

然后令x=a/c,y=b/c，直接三元降二元。。整理得

(u[i]-u[t])/u[i]/u[t]*y+(w[i]-w[t])/w[i]/w[t]*y+(v[i]-v[t])/v[i]/v[t]<=0

不推荐写1/u[i]-1/u[t]这类。。。貌似容易爆精度。。（评论区一大堆1e-16貌似就是这么来的。。

然后就剩下几个坑点了。。

要注意到题目要的是唯一胜者，交完出来是不是个点还需要特判。。。

另外。。x,y可能会非常大。。inf能开大就尽量开大。

/**
  poj 1175 #BFS
  BFS出每个云团，问题在于处理两个云团是否相同。
  处理方法是将每个云团映射到[0,0] 到[n,m]的矩阵中，然后就可以旋转或对称操作之后来比较了。
 */
#include <stdio.h>
#include <queue>
#include <algorithm>
#include <iostream>
using namespace std;

#define N 555
#define M 111
#define INF 55555
char mat[M][M];
struct Point
{
	int x,y;
	Point(int a = 0,int b = 0)
	{
		x = a;
		y = b;
	}
};
bool cmp(Point a,Point b)
{
	if(a.x == b.x)
		return a.y < b.y;
	return a.x < b.x;
}
struct node
{
	int m,n,x,y;
	vector<Point> vec;
	void draw(char c)
	{
		int len = vec.size();
		for(int i = 0; i < len; ++i)
			mat[x+vec[i].x][y+vec[i].y] = c;
	}
	
	void push(vector<Point> ve)
	{
		int minx,miny,maxx,maxy;
		minx = miny = INF;
		maxx = maxy = -1;
		int len = ve.size(),i;
		for(i = 0; i < len; ++i)
		{
			minx = min(minx,ve[i].x);
			miny = min(miny,ve[i].y);
			maxx = max(maxx,ve[i].x);
			maxy = max(maxy,ve[i].y);
		}
		n = maxx - minx + 1;
		m = maxy - miny + 1;
		x = minx;
		y = miny;
		for(i = 0; i < len; ++i)
			vec.push_back(Point(ve[i].x-x,ve[i].y-y));
		sort(vec.begin(),vec.end(),cmp);
	}
	void rotate()
	{
		int i,t,len = vec.size();
		for(i = 0; i < len; ++i)
		{
			t = vec[i].y;
			vec[i].y = n - vec[i].x - 1;
			vec[i].x = t;
		}
		swap(m,n);
		sort(vec.begin(),vec.end(),cmp);
	}
	void reservey()
	{
		int i,len = vec.size();
		for(i = 0; i < len; ++i)
		{
			vec[i].x = n - vec[i].x - 1;
		}
		sort(vec.begin(),vec.end(),cmp);
	}
	void reservex()
	{
		int i,len = vec.size();
		for(i = 0; i < len; ++i)
			vec[i].y = m - vec[i].y - 1;
		sort(vec.begin(),vec.end(),cmp);
	}
	
}c[N];
bool same(node t,node p)
{
	
	if(t.m == p.m && t.n == p.n && t.vec.size() == p.vec.size())
	{
		int i,len = t.vec.size();
		for(i = 0; i < len && t.vec[i].x == p.vec[i].x && t.vec[i].y == p.vec[i].y; ++i);
		return i == len;
	}
	return 0;
}
bool similars(node t,node p)
{
	node pt;
	if(t.m != p.m & t.n != p.n && t.m != p.n && t.n != p.m)
		return 0;
	for(int i = 0; i < 4; ++i)
	{
		
		if(same(t,p))
			return 1;
		pt = p;
		
		pt.reservey();
		if(same(t,pt))
			return 1;
		
		pt = p;
		pt.reservex();
		if(same(t,pt))
			return 1;
		
		p.rotate();
	}
	return 0;
}

int n,m;
bool ok(int x,int y)
{
	return x >= 0 && x < n && y >= 0 && y < m && mat[x][y] == '1';
}
vector<Point> bfs(int x,int y)
{
	vector<Point> vv;
	Point p(x,y),pt;
	queue<Point> que;
	int i;
	que.push(p);
	vv.push_back(p);
	mat[x][y] = '0';
	while(!que.empty())
	{
		p = que.front();
		que.pop();
		for(i = 0; i < 8; ++i)
		{
			int move[8][2] = {0,1, 1,0, 0,-1, -1,0, 1,-1, 1,1, -1,1, -1,-1};
			pt = Point(p.x+move[i][0],p.y+move[i][1]);
			
			if(ok(pt.x,pt.y))
			{
				que.push(pt);
				vv.push_back(pt);
				mat[pt.x][pt.y] = '0';
			}
		}
	}
	return vv;
}

int vis[N];
int main()
{
	scanf("%d%d",&m,&n);
	int i,j,k = 0;
	for(i = 0; i < n; ++i)
		scanf("%s",mat[i]);
	for(i = 0; i < n; ++i)
		for(j = 0; j < m; ++j)
			if(mat[i][j] =='1')
				c[k++].push(bfs(i,j));
	char ch = 'a';
	for(i = 0; i < k; ++i)
	{
		if(vis[i])
			continue;
		vis[i] = 1;
		c[i].draw(ch);
		for(j = i + 1; j < k; ++j)
			if(!vis[j] && similars(c[i],c[j]))
		{
			c[j].draw(ch);
			vis[j] = 1;
		}
		++ch;
	}
	for(i = 0; i < n; ++i)
		printf("%s\n",mat[i]);
	return 0;
}